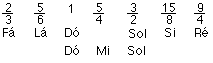
Intervalos justos são aqueles baseados em razões inteiras do tipo 3/2 (quinta), 4/3 (quarto), 2/1 (oitava), 5/4 (terça maior) e 6/5 (terça menor).
Se juntarmos um intervalo de terça maior justa com um intervalo de terça menor justa temos a proporção 4/5/6. Quaisquer 3 frequências que tenham essa proporção formam uma tríade maior, base do sistema tonal.
A construção de uma escala justa se dá pela superposição das tríades maiores justas (baseadas na proporção 4/5/6) Fá-Lá-Dó, Dó-Mi-Sol e Sol-Si-Ré.
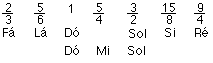
Mi-Sol-Si = (5/4) / (3/2) / (15/8) = 10:12:15
Lá-Dó-Mi = (5/3) / 2 / (5/2) = 10:12:15
(Note que 10/12 = 5/6 (terça menor) e 12/15 = 4/5 (terça maior).
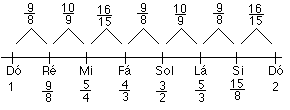
Embora a essa escala tenha 3 tríades maiores e 2 menores, todas com intervalos justos, existem problemas em relação aos outros intervalos. Por exemplo, a quinta Ré-Lá tem uma razão de (27/40), uma coma sintônica abaixo de um quinta justa. O intervalo Ré-Fá (27/32) é uma terça menor pitagórica e não uma terça menor justa. Portanto a tríade Ré-Fá-Lá está desafinada. Pela figura acima nota-se que o semitom justo tem a a razão (16/15), mas existem dois intervalos diferentes de tom, um com uma razão de (9/8) como na escala pitagórica e outro com a razão (10/9). Isso gera diferenças acentuadas nas notas enharmônicas impossibilitando a realização de mudanças de tonalidade ou modulações.
Embora a escala justa tenha sido considerada como a escala natural seu uso prático torna-se muito difícil em função dos desvios gerados por alguns intervalos.
atualizado em 20/01/2000